博弈论模型

标准式零和博弈

在双人标准式零和博弈中，每个博弈参与者选择一个行动，并根据博弈参与者自己的行动和另一个博弈参与者的行动获得一定收益。此外，博弈参与者双方的收益总和为零。如下图所示，在一个硬币配对博弈中，每个博弈参与者都要在两个行动中做出选择，他们分别是猜硬币正面朝上还是背面朝上：

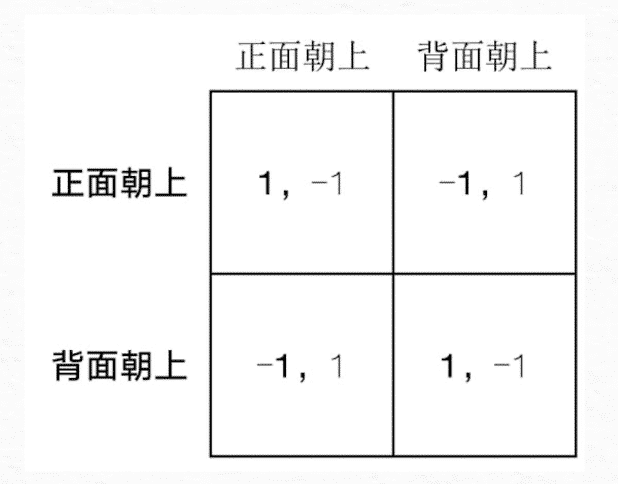
博弈的纳什均衡是指能够使每个博弈者的策略在给定其他博弈参与者策略的情况下是最优的。在硬币配对博弈中，存在一个唯一的均衡策略，那就是两个博弈者都以相同的概率在两个行动之间进行随机化。如果行博弈者以1/2的概率选择正面朝上、1/2的概率选择背面朝上，无论他的选择到底是什么，列博弈者的收益都为零。正因为如此，随机化是列博弈者的最优策略，根据对称性，随机化也是行博弈者的最佳选择。随机化策略的最优性，对策略互动环境中的行为有很大的意义。体育运动也是零和博弈，一方获胜，另一方就要落败。在所有的比赛中，任何非随机性都有可能会被对手利用。

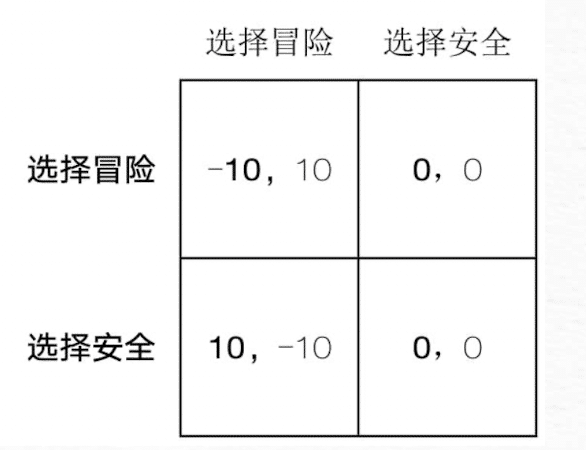
还有另外一种博弈，博弈者的收益不仅取决于自己的行动，还取决于哪个博弈者采取了哪一个行动。这是一个非对称零和博弈，每一个博弈者都可以选择冒险或安全的行动。在这个博弈中，行博弈参与者有一个占有策略，即采用安全的行动，如果行博弈者选择了安全的行动，那么列博弈者只有选择安全才会是最优解，如果行博弈者选择冒险，列博弈者作为后手可以直接得分。这种一方为另一方排除最优策略被称为迭代消除被占优策略，因此，两个博弈者都选择最安全的行为是这个博弈的纳什均衡。

序贯博弈

在序贯博弈中，博弈者按照特定顺序采取行动，由此可以用一颗博弈树来表示一个序贯博弈。博弈树由节点和边组成，每个节点对应于博弈者必须采取行动的时刻，该节点的每条边分别表示可以采取的某个行动。在博弈树最末尾的分支上，我们可以写下行动路径的收益。

在上图的博弈中，有两个参与者，分别是拟进入者和现有企业。如果拟进入者选择不进人市场，那么它的收益为零，现有企业收益为5。如果拟进入者决定进入市场，那么现有企业必须要做出选择，要么接受新进入者，要么与其发起商战。那么如何在这两个选项中做出选择呢？

我们可以用逆向归纳法来求解子博弈均衡，从最末端的节点开始，并在每个节点处选择最优行动，然后沿着博弈树逆向倒推，我们从现有企业末端节点倒推的最优行动就是接受对方进入，然后移动到博弈树上面的节点，也不难发现拟进入者的最优策略也是进入。虽然每个市场的进入和接受都是唯一子博弈的完美均衡，但实际上，这可能不会发生，我们在商战中通用的做法总是阻止其进入其他市场。

小结

零和博弈不包括互利的行动组合，在其中任何行为对一方收益，在数量上都等于对另一方的损，从一个人那里拿钱给另一个就是零和行动。我们应该是指探讨政策变化是否会导致零和博弈。