竞争模型

空间竞争模型

空间竞争模型假设备选项可以用一组属性来定义，消费者也可以用一系列理想点来定义。假设一些消费者分散在海滩山，海滩上有两个卖冰淇淋的小贩，每个消费者都会从离自己更近的那个小贩手中购买一个冰淇淋。下图中分割点位于这两个小贩的中点，它决定了哪些消费者会从哪个小贩手中购买冰淇淋。

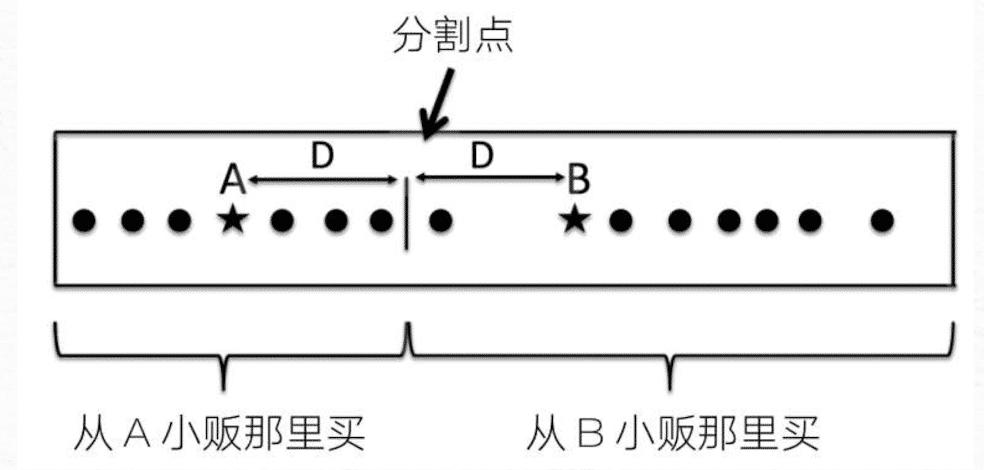
一般的空间竞争模型可以包括任意数量的属性，比如，沙发可以通过多个物理维度来描述：长度、宽度和结构类型等等。消费者从产品中获得的价值取决于产品在各个维度上与立项点的距离。最终消费者会根据与立项点的距离选择购买的商品。

在这种空间竞争模型中，对于两个巧克力，可以用可可的含量和含糖量表示属性，分割线是链接着两个产品直线的垂直平分线，理想点位于分割线左侧的消费者更喜欢A，立项点位于分割线右侧的更喜欢B。

享受竞争模型

在享受竞争模型中，各备选项也是用属性来表示的，但是，在这种模型中，属性包括了质量、效率或价格等内容，享受竞争模型允许个体给与不同维度赋予不同的权重。

利用线性回归方法，我们可以运用享受竞争模型推断商品属性的隐含价值，在模型中假设收益是商品属性和个人赋予权重的线性函数，如果我们获得了商品的售价以及关于这些商品属性的数据，就可以通过回归估计出购买房屋的人赋予每个属性的平均权重。这种方法也被称为享受回归。

空间竞争模型和享受竞争模型在如何表示对各种属性的偏好上有所不同，在空间竞争模型中，每个人对每种属性都有一个更偏好的水平，某个备选项在哪些维度上与他的理想点更接近，对他来说价值就越大。而在享受竞争模型中，每个属性越多（或越少），人们就越喜欢。

我们可以创建一个混合模型，让备选项同时包含空间属性和享受属性，这种模型可以用来分析市场进入、产品差异化竞争，以及价格竞争的激烈程度。在这个模型中，我们可以将现有产品放在属性空间中分析，通过问卷或其他的形式，了解消费者的理想点分布情况。我们可以将空间竞争模型中的降价行为视为分割线的移动，分割线位于不同商品之间无差异的消费者理想点。如果上述分析过的B巧克力企业进行了降价促销，并且消费者愿意付出更少的钱来获得同样多的糖果，那么必然这种降价会分割线推向A，并且使B市场份额增大。

价格变化在拥挤的市场和稀疏的市场中会产生不同的影响，在稀疏市场中，B巧克力价格下降10%，但是销量只增长了8%，综合起来使销售收入减少了3%，这种情况下降价就不是一个好的竞争策略。在拥挤的市场中，市场上可能会有多种不同的巧克力，这时价格下降后，B的绝对市场份额影响可能并不算大，但是这不大的增幅可能却代表B的市场份额有相当大的增长比例，所以最终总体销售收入会增加。

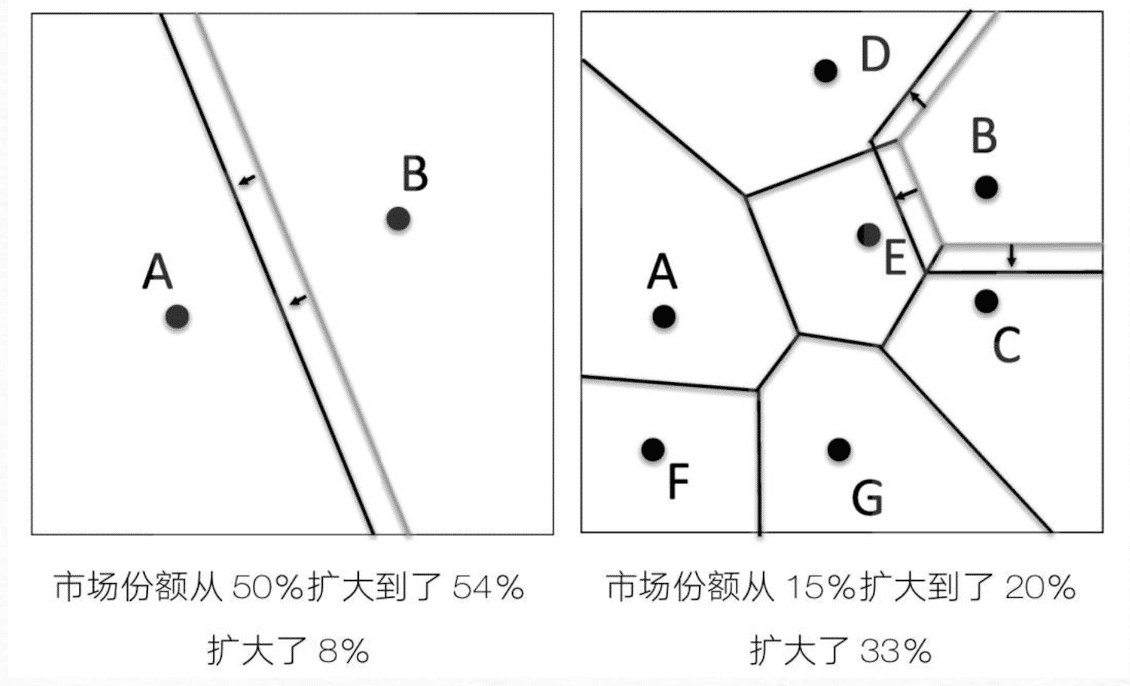
在这个模型中可以看出，拥挤市场中的价格竞争比稀疏市场的影响更大，高维性能创造出一个稀疏市场，在稀疏市场中商品价格竞争将很少出现。属性数量与价格竞争激烈程度之间这种关系表面，增加新属性可能会市市场更加稀疏，从而降低价格竞争的激烈程度，并带来更高的利润。