# 马尔可夫模型
马尔可夫模型用来刻画一定概率在一组有限的状态之间不断转换的系统。在马尔可夫模型中,状态之间转移发生的概率是固定的。如果系统可以通过一系列过渡从任何一个状态转换为任何其他状态,并且不存在简单的循环,那么马尔可夫模型就可以达到唯一的统计均衡。
在统计均衡中,单个实体可以继续在各种状态之间移动,但是各种状态之间的概率分布仍然是固定的。例如,一个关于意识形态的,马尔可夫模型,统计均衡允许人们在持自由主义立场、保守主义立场和中立立场之间转换,但是秉持每种意识形态的人口比例将保持不变。在应用于单一实体时,统计均衡意味着实体处于每种状态的长期概率不会改变。例如,当一个人处于统计均衡状态时,他在60%的时间内感到高兴,而在40%的时间里感到悲伤。这个人的精神状态可能每小时都会发生变化,但是他在这些精神状态之间的长期分布却不会发生变化。
这种独特的统计均衡还意味着,结果的长期分布不可能取决于初始状态或事件的路径,初始条件是无关紧要的,历史也是无关紧要的,会改变状态的干预措施也不重要,随着时间的推移,满足这些假设的过程就会走向一个独特的统计均衡,然后保持不变。
# 马尔可夫模型的应用
马尔可夫模型由一组状态与这些状态之间的转移概率构成。假设这些转移概率适用于100名学生,学生有90%的机会停留在充实的状态上,有10%的概率会觉得无聊,当无聊时,这个学生有30的几率变得充实。当这些学生中第一天有一半学生觉得学习令他们很充实,另一半学生则觉得很无聊。应用转移概率,可以预计第二天会有5名原本充实的学生会变得无聊,同时会有15名无聊的学生变得充实。持续运用这个转移规则,这个马尔可夫过程会收敛到75名同学觉得充实,25名同学觉得无聊的统计均衡。在这个统计均衡中,学生们会继续在这两种状态之间转移,但是处于每一种状态的学生总数保持不变。
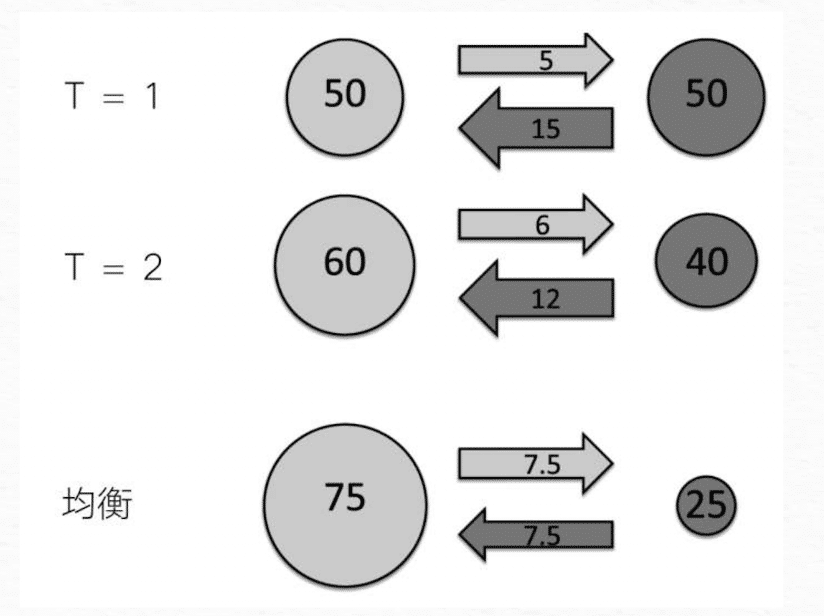
假设这个过程开始时,所有100名同学的状态都是充实,继续迭代这个过程可以发现,从长远看,最终仍然会收敛到75名学生觉得充实,25名学生觉得无聊的统计均衡。
# 佩龙-弗罗宾尼斯定理
任何一个马尔可夫模型,只要状态集是有限的、不同状态之间的转移概率是固定的、在一系列转以后能够从任何一个状态变换为任何其他状态,而且状态之间不存在固定的循环,就必定会收敛到唯一的统计均衡。这个定理意味着,如果满足这四个假设,那么改变初始状态、历史和干预措施,都不能改变长期中的均衡。
佩龙-弗罗宾尼斯定理说明了一个马尔可夫模型必定收敛于一个唯一的统计均衡要满足的条件:
- 有限状态集:S={1,2,...,K}
- 固定转换规则:状态之间的转移概率是固定的,即在每个周期中,从状态A转换为状态B的概率总是等于P(A,B)。
- 状态可达性:系统可以通过一系列转换从任何状态到达任何状态。
- 非循环性:系统不会通过一系列状态产生确定的循环。
有一种销量-耐久性悖论,它说产品或创意的流行程度与其说取决于他们的相对销量,不如说取决于他们的耐久性。只需要将某种类型商品人的比例设定为状态,就可以用马尔可夫模型解释这个悖论。在这个模型中,假设油毡的销量是瓷砖的3倍,每年有1/10的人必须要更换油毡,而需要换瓷砖的人只有1/60,由此可以得到的马尔可夫模型的均衡中,最终有2/3的地板都是用瓷砖铺成的。
# PageRank算法
谷歌运用马尔可夫模型构造了最初的网页排名算法PageRank。万维网由链接连接起来的网站组成,为了估算出每一个站点的相对重要性,可以计算一个站点连入和接出的链接数量,通过链接数量粗略估计站点的重要性。如下图所示的站点网络中,站点B、C、E各有两个链接,A有一个链接,D没有链接:

网页排名算法将每个站点都视为一个马尔可夫模型中的状态,如果两个站点共享一个链接,那么就在这两个站点之间分配一个正的转移概率。我们暂且为任何链接分配相等的概率,假设在A上的搜索者有同样的可能性移动到B或者E上,如果搜索者来到了E上,那么将永远交替出现在C和E之间。如果搜索者选择了B,那么他还是会去C,然后再一次开始C和E之间交替出现。实际上,从任何站点开始都会导致交替出现在C和E之间这个结果,我们发现C和E似乎是更加重要的站点,但是它不满足佩龙-弗罗宾尼斯定理的假设。该系统无法从任何站点达到任何其他站点,而且转移概率在C和E之间创建了一个循环。
谷歌的算法为了解决这一问题,加入了一点:从任何站点都能够以一个很小的随机概率移动到任何其他站点。于是所有的站点都可以根据它们在哪个均衡中的概率进行排序,从A开始的搜索者,最后可能在几次搜索后达到C或E结束,一旦达到C或E后,他将会在这两个站点之间反复来回,直达尝试签一个随机站点为止。如果他到了A或者D,那么回到C的路径很可能会经过B或者E。因此,B的排名应该高于A或D。

网页排名可以看做随机游走与马尔可夫模型的组合,如果将网页排名视为一种算法,就会发现可以用它来生成任何网络的排名,我们可以让节点代表一支球队,再用转移概率表示一只球队击败另外一只球队的时间百分比。
# 小结
马尔可夫模型描述了以固定的转移概率在不同状态之间转换的动态系统。如果再假设这个过程能够在任何两个状态之间转移,并且这个过程不会产生循环,那么马尔可夫模型就可以得到唯一的统计均衡。在均衡中,人或实体在各个状态之间移动,但是各个状态的概率分布不会发生变化,由此可见,当一个过程接近均衡时,概率变化就会减弱。
在应用马尔可夫模型解释现象或者预测趋势时,缄默症对状态的选择至关重要,系统会存在一个唯一的统计平衡,系统状态的任何一次变化都只能产生一些暂时性的影响。因此我们可以推断,那些试图通过一两天的活动来激发人们学习兴趣的做法,可能不会产生什么有意义的影响。任何一次性的资金涌入,无论其规模大小,影响最终都会消失,除非可以改变其转移概率。
然而,并不是每一个动态系统都满足马尔可夫模型,在不满足马尔可夫模型假设的情况下,历史、干预政策和事件都可能会产生长期影响。例如,在波利亚过程中,结果改变了长期均衡,对系统的重大干预或冲击可能会改变转移概率甚至是整个状态集。因此,我们也许更应该将历史视为一个马尔可夫模型序列,而不是视为一个向不可避免的均衡方向发展的过程。