崎岖景观模型

与空间竞争模型和享受模型一样，崎岖景观模型也将一个实体定义为属性的集合，每个属性的集合都映射到一个价值上。崎岖景观模型的目标是修改属性，以构造出一个具有最高价值的实体。

合适度景观模型

合适度景观模型假设物种有用能够促进其合适度的特征或形状，同时种群中不同成员所拥有的特定形状数量或程度可能不同。如果用横轴表示形状，用纵轴表示物种的合适度，就可以会出一张合适度景观的图，其中高海拔点对应高合适度。

以土狼为例，我们令土狼的所有其他形状都保持不变，只改变它尾巴的长度，并测量尾巴长度变化对合适度的影响。假设一只土狼的尾巴有助于在跳跃时保持平衡，而土狼可以将它作为对外传递的某种信号。我们从横轴最左侧开始，那里尾巴长度为零，这种情况下它不能执行任何功能，随着尾巴的长度增加，维持平衡和传递信号的功能也随之提高，如果尾巴变得过长，可能土狼运动的敏捷度会下降，所以一旦尾巴超过某个临界值，合适度就会下降，如下图所示：

、

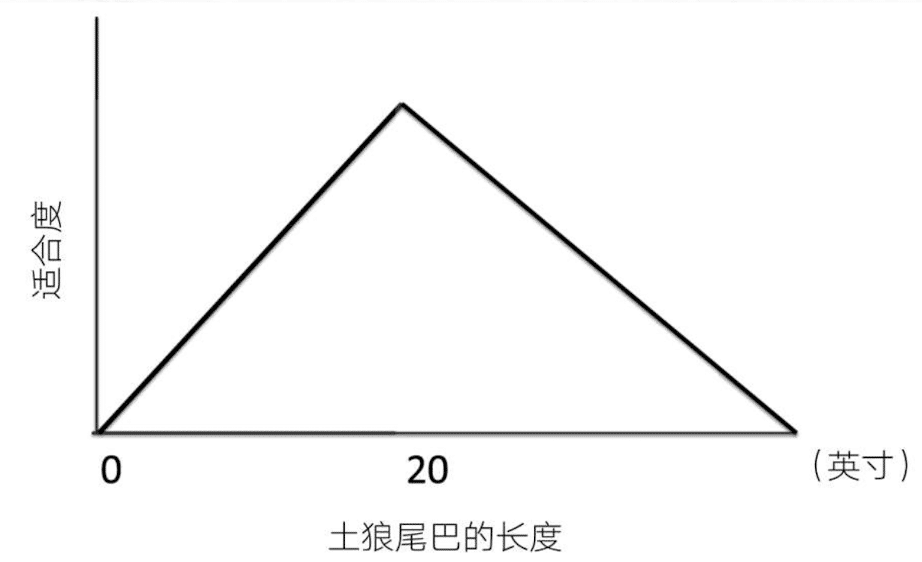
这种单峰景观被称为富士山景观，有富士山景观的问题通常都是比较容易解决的问题，我们可以应用一对多的思维方法，将这个问题重新解释为一个产品设计问题。从表面上看，景观模型将合适度、效率或价值作为特征和性状的函数绘制在了图上，然后爬上山顶找到特征和性状的最优值。但是，当我们同时考虑多个属性并且允许一个属性的贡献与其他属性的贡献相互作用时，就会产生另一种景观。

崎岖景观

当我们考虑设计一个沙发的问题，就必须要决定坐垫的厚度和扶手的宽度，我们用沙发在市场上的预期销售额来代表设计的价值，而沙发的销售额与设计的美感也相关。如果沙发有厚厚的垫子，那么较为宽阔的扶手可能会使沙发更具美感，如果沙发的垫子很薄，那么扶手窄一点会更好。作为扶手宽度和坐垫厚度的函数，预期销售的二维图将具有两个山峰，一个山峰用于窄扶手、薄垫子，另一个山峰用于宽扶手，厚垫子的沙发设计。

变量之间的相互依赖效应，使得景观出现了崎岖的特点，这种崎岖性有几个重要的含义。首先，在崎岖景观只能怪寻找到最高点时所用的不同方法，可能会以找到不同山峰而告终，如果从不同的起点出发，可能会找到不同的山峰，因此，崎岖性导致了对初始条件的敏感性和路径依赖的可能性。这些意味着，景观的崎岖性有助于结果的多样性，崎岖性也意味着出现次优结果的可能性，在崎岖景观中，次优结果表现为局部高峰。

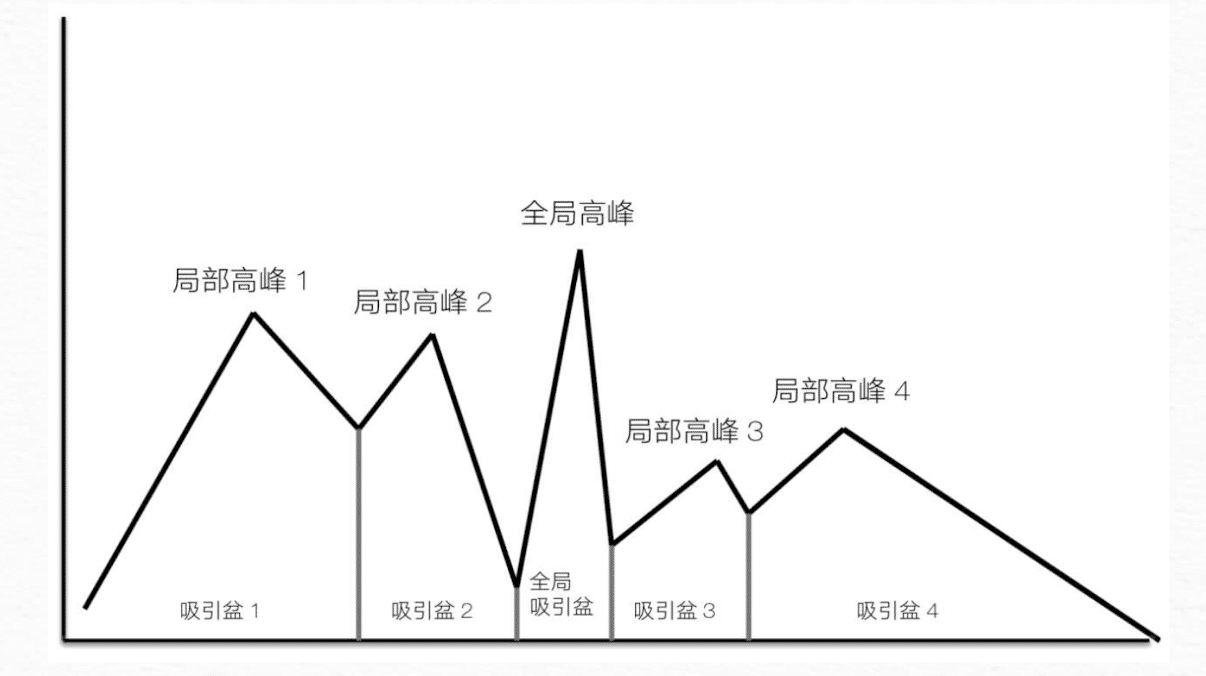
在崎岖景观中找到最优或接近最佳的高峰，需要多样性和复杂性的方法。如果不同的启发式能够找到不同的峰值，那么对一个问题应用多个不同启发式就能产生多个不同的局部峰值，然后就可以从这些局部峰值中选择一个最优解。如果不同的起点应用同一个启发式，那么先找到若干个不同的局部最优点，然后选择其中最优解也能得到相同的结果。