广播、扩散、传染模型

广播模型都将整个群体划分为两个群组，分别是：知道或拥有某种东西的人和不知道或不拥有某种东西的人。随着时间推移，个人会在这两个群组之间移动，有人会从易感者变成感染者，或者从不了解新产品新思想的人变成知情达意者。

广播模型要假设存在一个相关人群，用Npop表示，在任何时候总会有些人患上了某种传染病，或者想了解特定的信息，疑惑已经采取了一定的行动，我们将这些人称为感染者或知情者（用It表示），相关人群中除了感染者或知情者之外的其余成员是易感者（用St表示），这些易感者可能会感染传染病、了解信息或采取行动。相关人群的总人数等于感染者或知情者人数加上易感者人数的总和：Npop=It+St。

广播模型的公式为：It+1=It + Pbroad * St，其中Pbroad表示广播概率，It和St分别等于时间t上的感染者（知情者）和易感者的数字，初始状态为I0=0，且S0=Npop。

广播模型刻画了思想、谣言、信息或技术通过电视、广播、互联网等媒体进行的传播。大多数实时新闻都是通过广播形式传播的，这个模型的目标是描述一个信息源传播信息的过程，可以是政府、企业或报纸。

广播模型说明在给定时间段内，知情者人数等于前一期的知情者人数加上易感者听到信息的概率乘以易感者人数，要计算未来某期的知情者人数，只需要将知情者和易感者人数代入方程即可，由此得到的是一个r形采用曲线。假设某个拥有100万居民的城市宣布了一项新的税收政策，在他宣布之前没有人知道政策，如果人在任何一天听到这个新闻的概率是30%，那么第一天会有30万人听到这个新闻，第二天剩下70万人中有30%，即21万人会听到这个新闻，在每一个时期知情人数都会呈递减速度增加。在广播模型中，相关人群中在理想情况下最终都会知悉信息，如果有适当的数据，就可以估算出相关人群的规模。

扩散模型

大多数传染病，以及关于产品、思想和技术突破的信息，都是通过口口相传而传播开来的，扩散模型刻画了这些过程。扩散模型假设，当一个人采用了某种技术或患上某种传染病时，这个人有可能将之传递或传染给其他接触的人。在这种情况下，个人选择不会在其中发挥任何作用，一个人患上传染病的概率取决于诸如遗传、病毒、甚至环境等因素。

我们可以将扩散概率定义为接触概率和分享概率的乘积，我们根据扩散概率来构建模型，但是在估计或应用模型时，必须独立地跟踪接触概率和分享概率。扩散模型假定随机混合，随机混合的含义是，相关群体中任何两个人接触的可能性都相同。扩散模型公式如下：

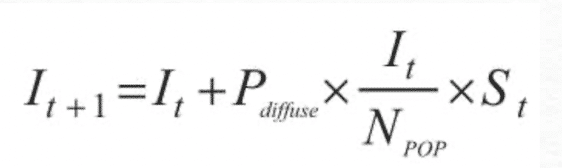
在这个模型中，与在传播模型中一样，长期看来，相关人群中的每一个人都会掌握信息，不同的是，扩散模型采用的曲线是S形的。最初几乎没有人知情，因此能够与知情者接触的易感人数也必定很小，随着知情者的人数增加，知情者与不知情者之间接触的机会增加，这又使知情者的人数更快的增多，当相关人群中几乎每个人都成了知情者时，新知情的人数会减少，从而形成了S形的顶部。

在使用扩散模型来指导行动的时候，我们必须将扩散概率分解为分享概率和接触概率的乘积。通过这个模型我们可以看出，如果是估算销量，那么总销量等于相关人群的规模，它与分享概率高低无关，提高销售速度不会带来长期的影响。

大多数消费品和信息都是通过广播和扩散传播的，巴斯模型将这两个过程组合在了一起。在巴斯模型中，扩散概率越大，采用曲线的S形就越显著。巴斯模型的公式如下：

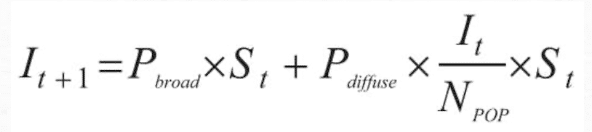
传染模型

在扩散传播的实践中，还有一种我们生活中比较常见的形态，就是传染病的感染，我们在患上某种传染病之后，经过治疗就会恢复健康，由此可以产生一种由易感者、传染者和痊愈者组成的新的模型--SIR模型。

SIR模型会产生一个临界点，就是基本再生数R0，它代表接触概率乘以扩散概率与痊愈概率之比。如果某种传染病R0大于1，那么这种传染病就可以传遍整个人群，而R0小于1最终传染病会趋于消失。在这个模型中，信息并不一定回传播到整个相关人群，能不能做到这一点取决于R0的值。

除了用SIR模型分析传染病传播，我们也可以将它用于所有线通过扩散传播，然后趋于消失的社会现象，例如商品的销售、文化的流行、热词的传播等等。在这些情形下，我们可以估计接触概率，传播率和痊愈概率，以及基本再生数R0。这个模型意味着，这些概率只要发生微小的变化，就可以使R0移动到高于零的水平，从而造成巨大的差别。