随机模型

如果不收集数据，随机性是很难辨别的，我们经常想当然的认为能够在选举结果、股票价格和体育赛事得分中总结出一定的模式，但这可能是我们一厢情愿的结果。

伯努利瓮模型

伯努利瓮模型由一个装了灰球和白球的瓮组成，从瓮中抽取的球代表随机事件的结果，每次抽取都与之前和之后的抽取无关，因此我们可以应用大数定律：从长远看，抽出每种颜色球的比例将会收敛到这个球在瓮中的比例。

伯努利瓮模型的结果产生了可预测长度的条纹，在灰球和白球数量相等的瓮中，抽取白球的概率等于1/2，连续抽取两个白球的概率等于1/2乘以1/2，以此类推，如果瓮中白球的比例为P，那么连续抽取N个白球的概率就等于P的N次方。通过概率，我们可以评估某种条纹是不是有可能出现，或者是几乎完全不可能出现。我们可以利用类似的计算来确定某一事件到底是幸运、能力出众还是欺诈。

随机游走模型

随机游走模型是建立在伯努利瓮模型的基础上，将过去结果的和保持下来建立的。我们将模型的初始值设置为零，如果我们抽取出一个白球，就在总数上加一，如果抽取出一个灰球就在总数上减一，模型在任何时候的状态都等于先前结果的总和，也就是抽取出来的白球总数减去抽取出来灰球总数的值。

下图给出了一个简单的随机游走，这幅图看上去有一个模式，它显示一个长期的下降趋势，然后是一个上升趋势，在上升过程中越过零线时出现了一个适度的崩溃。

简单的随机游走既有周期性的，它会无限次的返回零点，也有无界性，它会超过任何正的和负的阈值。返回零点所需的步数满足幂律分布。如果我们将企业的销售水平或员工规模建模为随机游走，那么企业的生命周期就会成为一个幂律分布，当销售强力的时候，企业会招聘一名新员工，当销售不佳时，会截屏员工，当企业不再拥有员工时，可能就会面临倒闭。企业是生命周期就是一个幂律。

这个基本随机游走模型可以通过多种方式加以修正，我们可以创建一个正态随机游走，在正态随机游走中，每一周期值的变化都服从正态分布，正态随机游走不会完全回到零点，但它会无限次的穿过零点。我们还可以另某一种结果比另一种结果更有可能发生，从而创建一个有偏差的随机游走。

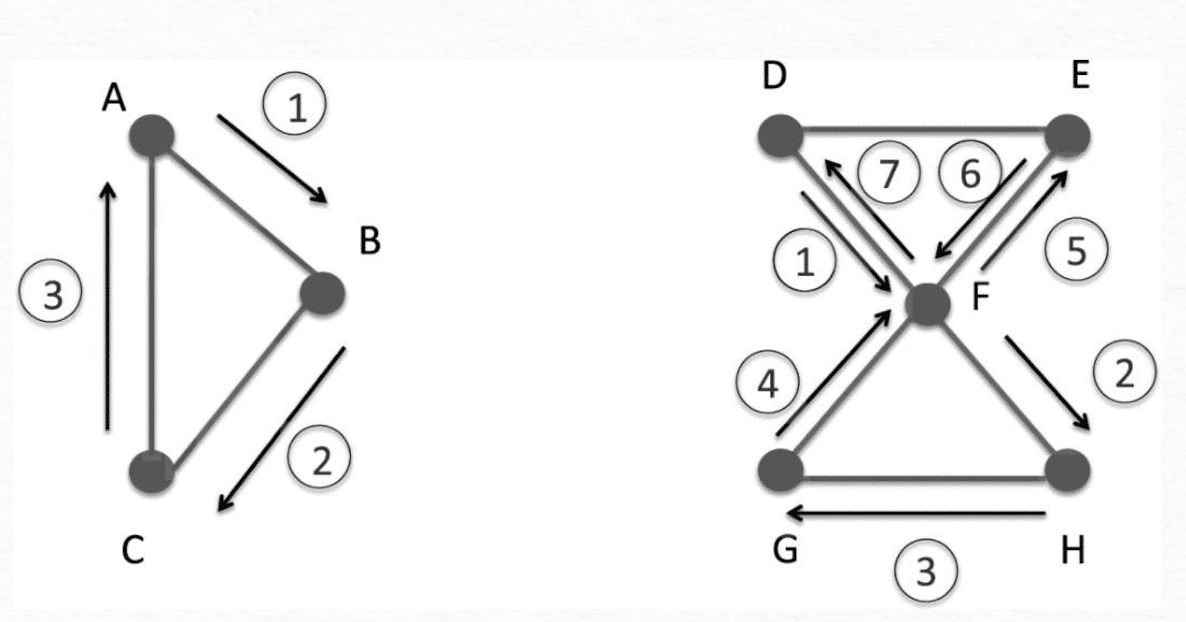
利用低维随机游走的递归性来估计某个网络的规模，我们随机选择一个节点，然后沿着网络的边开始随机游走，并跟踪它回到初始节点的频率。返回到初始节点所需的平均时间与网络的规模相关。下图显示了两个网络，左边网络由3个节点组成了一个三角形，右边网络有6个节点，组成了两个三角形。在左边我们从A开始随机游走，只需要3步就可以返回起点。在右边的网络上，随机游走要7步才能回到起点,对于大型网络我们可以利用这种方式来评估网络规模。

经济学家基于随机游走思想进行拓展，提出了有效市场假说。这个假说指出，在任何时候股票价格都反映了所有的相关信息，为了的价格必定遵循随机游走。